Giải câu 3 bài 3: Hàm số liên tục
Câu 3: trang 141 sgk toán Đại số và giải tích 11
Cho hàm số ![]()
a) Vẽ đồ thị của hàm số ![]() . Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.
. Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.
b) Khẳng định nhận xét trên bằng một chứng minh.
Bài làm:
a. Đồ thị hàm số ![]() là một đường không liền nét mà bị đứt quãng tại \(x_0= -1\).
là một đường không liền nét mà bị đứt quãng tại \(x_0= -1\).
Vậy hàm số đã cho liên tục trên khoảng ![]() và \((- 1; +∞)\).
và \((- 1; +∞)\).
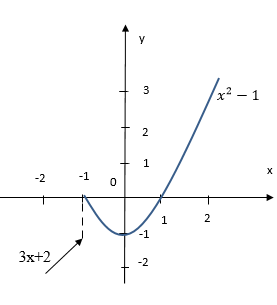
b.
- Nếu
 : \(f(x) = 3x + 2\) liên tục trên \((-∞; -1)\) (vì đây là hàm đa thức).
: \(f(x) = 3x + 2\) liên tục trên \((-∞; -1)\) (vì đây là hàm đa thức). - Nếu
 : \(f(x) = x^2- 1\) liên tục trên \((-1; +∞)\) (vì đây là hàm đa thức).
: \(f(x) = x^2- 1\) liên tục trên \((-1; +∞)\) (vì đây là hàm đa thức). - Tại
 ;
;
Ta có:
![]()
![]()
Vì ![]()
Vậy không tồn tại ![]() .
.
Vậy hàm số gián đoạn tại ![]() .
.
Xem thêm bài viết khác
- Giải bài 4 Ôn tập cuối năm
- Phần bài tập Ôn tập cuối năm
- Giải bài 16 bài ôn tập chương 3: Dãy số, cấp số cộng và cấp số nhân
- Giải câu 4 bài 3: Cấp số cộng
- Giải câu 7 bài Ôn tập chương 5: Đạo hàm
- Giải câu 5 bài 4: Phép thử và biến cố
- Giải câu 1 bài 4: Cấp số nhân
- Giải câu 5 bài 3: Hàm số liên tục
- Giải câu 1 bài 3: Cấp số cộng
- Giải bài Ôn tập chương 3: Dãy số, cấp số cộng và cấp số nhân
- Giải bài 7 Ôn tập cuối năm
- Giải câu 10 bài ôn tập chương 3: Dãy số, cấp số cộng và cấp số nhân











