Giải câu 6 bài ôn tập chương 4: Giới hạn

1 Đánh giá

Câu 6: trang 142 sgk toán Đại số và giải tích 11

Cho hai hàm số $f(x) = {{1 - {x^2}} \over {{x^2}}}$ và $g(x) = {{{x^3} + {x^2} + 1} \over {{x^2}}}$

a) Tính $\mathop {\lim }\limits_{x \to 0} f(x);\mathop {\lim }\limits_{x \to 0} g(x);\mathop {\lim }\limits_{x \to + \infty } f(x);\mathop {\lim }\limits_{x \to + \infty } g(x)$

b) Hai đường cong sau đây (h.60) là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem đường cong nào là đồ thị của mỗi hàm số đó.

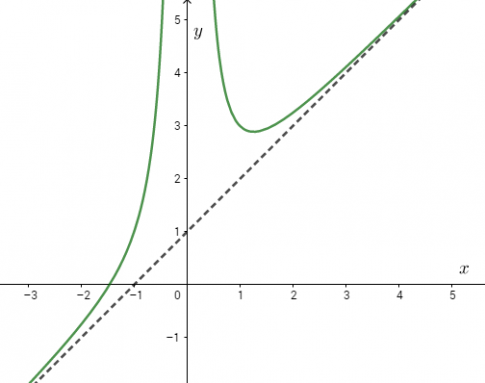
Hình 60 a

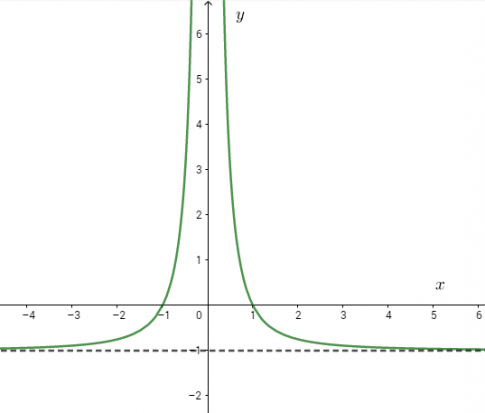
Hình 60 b

Bài làm:

Vì $\mathop {\lim }\limits_{x \to 0} (1 - {x^2}) = 1 > 0,\mathop {\lim }\limits_{x \to 0} {x^2} = 0;{x^2} > 0,\forall x \ne 0$

$\Rightarrow \mathop {\lim }\limits_{x \to 0} f(x) = \mathop {\lim }\limits_{x \to 0} {{1 - {x^2}} \over {{x^2}}} = + \infty$

Vì $\mathop {\lim }\limits_{x \to 0} ({x^3} + {x^2} + 1) = 1 > 0,\mathop {\lim }\limits_{x \to 0} {x^2} = 0,{x^2} > 0,\forall x \ne 0$

$\Rightarrow \mathop {\lim }\limits_{x \to 0} g(x) = \mathop {\lim }\limits_{x \to 0} {{{x^3} + {x^2} + 1} \over {{x^2}}} = + \infty$

Ta có: $\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } {{1 - {x^2}} \over {{x^2}}}$

$= \mathop {\lim }\limits_{x \to + \infty } {{{x^2}({1 \over {{x^2}}} - 1)} \over {{x^2}}} = \mathop {\lim }\limits_{x \to + \infty } \left ( {1 \over {{x^2}}} - 1 \right ) = - 1$

Ta có: $\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } {{{x^3} + {x^2} + 1} \over {{x^2}}} = \mathop {\lim }\limits_{x \to + \infty } {{{x^3}(1 + {1 \over x} + {1 \over {{x^3}}})} \over {{x^3}({1 \over x})}}$

$= \mathop {\lim }\limits_{x \to + \infty } {{1 + {1 \over x} + {1 \over {{x^3}}}} \over {{1 \over x}}} = + \infty$

b) Gọi $(C_1)$ và $(C_2)$ lần lượt là hai đồ thị của hàm số $y = f(x)$ và $y = g(x)$

Vì $\left\{ \matrix{ \mathop {\lim }\limits_{x \to 0} f(x) = + \infty \hfill \cr \mathop {\lim }\limits_{x \to 0} g(x) = + \infty \hfill \cr} \right.$

nên hai đồ thị $(C_1)$ và $(C_2)$ có nhánh đi lên khi $x \rightarrow 0$.

Vì $\mathop {\lim }\limits_{x \to + \infty } f(x) = - 1$ nên $(C_1)$ có nhánh tiến gần đến đường thẳng $y = -1$khi $ x \rightarrow ∞$. Ta thấy giống đặc điểm của đồ thị b
Vì $\mathop {\lim }\limits_{x \to + \infty } g(x) = + \infty$ $(C_2)$ có nhánh đi lên khi $x \rightarrow +∞$. Ta thấy giống đặc điểm của đồ thị a.

Vậy đồ thị hình b là đồ thị của hàm số $f(x) = {{1 - {x^2}} \over {{x^2}}}$ và hình a là đồ thị của hàm số $g(x) = {{{x^3} + {x^2} + 1} \over {{x^2}}}$

lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Đại số và giải tích lớp 11