Giải bài 1: Phương pháp quy nạp toán học
Dựa theo cấu trúc SGK toán lớp 11, KhoaHoc xin chia sẻ với các bạn bài: Phương pháp quy nạp toán học. Với kiến thức trọng tâm và các bài tập có lời giải chi tiết, hi vọng rằng đây sẽ là tài liệu giúp các bạn học tập tốt hơn.
Nội dung bài viết gồm 2 phần:
- Ôn tập lý thuyết
- Hướng dẫn giải bài tập sgk
A. LÝ THUYẾT
Phương pháp quy nạp toán học:
Để chứng minh một mệnh đề P(n) là đúng với mọi n Є N*, ta thường dùng phương pháp quy nạp toán học, được tiến hành theo hai bước như sau:
- Bước 1 (bước cơ sở): Kiểm tra mệnh đề P(n) đúng với n = 1.
- Bước 2 ( bước quy nạp): Giả thiết mệnh đề P(n) đúng với một số tự nhiên bất kì n = k, (k ≥ 1) (ta gọi là giả thiết quy nạp) và chứng minh rằng nó cũng đúng với n = k + 1.
Chú ý:
Nếu phải chứng minh một mệnh đề là đúng với mọi số tự nhiên n ≥ p (p là số tự nhiên) thì:
- Ở bước 1, ta kiểm tra mệnh đề đúng với n = p.
- Ở bước 2, ta giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k, (k ≥ p) và chứng minh rằng nó cũng đúng với n = k + 1.
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
Câu 1: Trang 82 - sgk đại số và giải tích 11
Chứng minh rằng với n Є N*, ta có đẳng thức:
a) 2 + 5+ 8+.... + 3n - 1 = ![]() ;
;
b) ![]() ;
;
c) 12 + 22 + 32 +….+ n2 = ![]() .
.
Câu 2: Trang 82 - sgk đại số và giải tích 11
Chứng minh rằng với n ε N* ta luôn có:
a) n3 + 3n2 + 5n chia hết cho 3;
b) 4n + 15n - 1 chia hết cho 9;
c) n3 + 11n chia hết cho 6.
Câu 3: Trang 82 - sgk đại số và giải tích 11
Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có các bất đẳng thức:
a) 3n > 3n + 1;
b) 2n + 1 > 2n + 3
Câu 4: Trang 83 - sgk đại số và giải tích 11
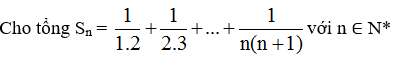
a) Tính S1, S2, S3.
b) Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
Câu 5: Trang 82 - sgk đại số và giải tích 11
Chứng minh rằng số đường chéo của một đa giác lồi n cạnh là ![]()
=> Trắc nghiệm đại số và giải tích 11 bài 1: Phương pháp quy nạp toán học
Xem thêm bài viết khác
- Giải câu 2 bài ôn tập chương 4: Giới hạn
- Giải câu 13 bài ôn tập chương 4: Giới hạn
- Giải bài 2: Quy tắc tính đạo hàm
- Giải bài 5: Xác suất của biến cố
- Giải câu 10 bài ôn tập chương 4: Giới hạn
- Giải bài 1: Phương pháp quy nạp toán học
- Giải câu 11 bài ôn tập chương 3: Dãy số, cấp số cộng và cấp số nhân
- Giải câu 8 bài ôn tập chương 4: Giới hạn
- Toán 11: Đề kiểm tra học kì 2 dạng trắc nghiệm (Đề 1)
- Giải bài 2 Ôn tập cuối năm
- Giải câu 5 bài 2: Phương trình lượng giác cơ bản
- Giải bài 16 Ôn tập cuối năm











