Giải bài 5: Phương trình mũ. Phương trình Lôgarit

Bài học với nội dung kiến thức về Phương trình mũ, phương trình Lôgarit. Một kiến thức không quá khó song đòi hỏi các bạn học sinh cần nắm được lý thuyết. Dựa vào cấu trúc SGK toán lớp 12, KhoaHoc sẽ tóm tắt lại hệ thống lý thuyết và hướng dẫn giải các bài tập 1 cách chi tiết, dễ hiểu. Hi vọng rằng, đây sẽ là tài liệu hữu ích giúp các em học tập tốt hơn

A. Tổng hợp kiến thức

I. Phương trình mũ cơ bản

1. Khái niệm

• Dạng tổng quát:

, $a>0,a\neq 1$

• Phương pháp giải:

Để giải phương trình mũ trên, ta áp dụng định nghĩa Lôgarit:

• 
• => Phương trình vô nghiệm.

• Đồ thị minh họa:

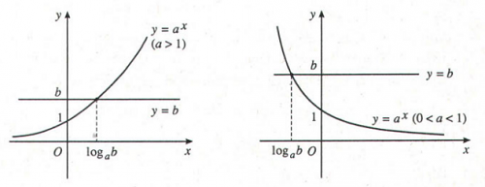
Tổng quát

2. Một số cách giải phương trình mũ cơ bản

• Đưa về cùng cơ số
• Đặt ẩn phụ
• Lôgarit hóa

II. Phương trình Lôgarit

1. Khái niệm

• Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit
• Dạng tổng quát:

, ( $a>0,a\neq 1$)

• Phương pháp giải:

Để giải phương trình lôgarit trên, ta áp dụng định nghĩa Lôgarit:

• Đồ thị minh họa:

Tổng quát

• Phương trình , ( $a>0,a\neq 1$) luôn có nghiệm duy nhất $x=a^{b}$ với mọi $b$.

2. Một số cách giải phương trình lôgarit đơn giản

• Đưa về cùng cơ số
• Đặt ẩn phụ
• Mũ hóa