Giải bài 2: Giới hạn của hàm số

1 Đánh giá

Bài 1 chúng ta đã được tìm hiểu về giới hạn của dãy số. Vậy còn giới hạn của hàm số là gì? Để giải đáp câu hỏi này, KhoaHoc xin chia sẻ với các bạn bài 2: Giới hạn của hàm số. Với lý thuyết và các bài tập có lời giải chi tiết, hi vọng rằng đây sẽ là tài liệu hữu ích giúp các bạn học tập tốt hơn.

Nội dung bài viết gồm 2 phần:

Ôn tập lý thuyết

Hướng dẫn giải bài tập sgk

A. Tóm tắt lý thuyết

I. Giới hạn hữu hạn của hàm số tại một điểm

1. Định nghĩa

ĐỊNH NGHĨA 1

Cho khoảng K chứa điểm $x_{0}$ và hàm số $y=f(x)$xác định trên K hoặc K \ { $x_{0}$ }

Ta nói hàm số $y=f(x)$ có giới hạn là số L khi x dần tới $x_{0}$ nếu với dãy số $(x_{n})$bất kì,

$x_{n}\in$ K \ { $x_{0}$ }; $x_{n}\rightarrow x_{0}$

ta có $f(x_{n})\rightarrow L$

Kí hiệu: $\underset{x\rightarrow x_{0}}{lim }f(x) = L$ hay $f(x)\rightarrow L$khi $x\rightarrow x_{0}$

2. Định lí về giới hạn hữu hạn

ĐỊNH LÍ 1

a. Giả sử $\underset{x\rightarrow x_{0}}{lim }f(x) = L$ và $\underset{x\rightarrow x_{0}}{lim }g(x) = M$

Khi đó:

$\underset{x\rightarrow x_{0}}{lim }[f(x)+g(x)] = L+M$
$\underset{x\rightarrow x_{0}}{lim }[f(x)-g(x)] = L-M$
$\underset{x\rightarrow x_{0}}{lim }[f(x).g(x)] = L.M$
$\underset{x\rightarrow x_{0}}{lim }\frac{f(x)}{g(x)} = \frac{L}{M}$ (nếu $M\neq 0$)

b. Nếu $f(x)\geq 0$ và $\underset{x\rightarrow x_{0}}{lim }f(x) = L$thì:

$L\geq 0$ và $\underset{x\rightarrow x_{0}}{lim }\sqrt{f(x)} = \sqrt{L}$

(Dấu của $f(x)$ được xét trên khoảng đang tìm giới hạn, với $x\neq x_{0}$)

3. Giới hạn một bên

ĐỊNH NGHĨA 2

Cho hàm số $y=f(x)$ xác định trên khoảng $(x_{0}; b)$

Số L được gọi là giới hạn bên phải của hàm số $y=f(x)$ khi $x\rightarrow x_{0}$nếu với dãy số $(x_{n})$bất kì, \(x_{0}

ta có $f(x_{n})\rightarrow L$

Kí hiệu: $\underset{x\rightarrow x_{0}^{+}}{lim }f(x) = L$

Cho hàm số $y=f(x)$ xác định trên khoảng $(a; x_{0})$

Số L được gọi là giới hạn bên trái của hàm số $y=f(x)$ khi $x\rightarrow x_{0}$nếu với dãy số $(x_{n})$bất kì, \(a

ta có $f(x_{n})\rightarrow L$

Kí hiệu: $\underset{x\rightarrow x_{0}^{-}}{lim }f(x) = L$

ĐỊNH LÍ 2

$\underset{x\rightarrow x_{0}}{lim }f(x) = L$ khi và chỉ khi $\underset{x\rightarrow x_{0}^{-}}{lim }f(x) = \underset{x\rightarrow x_{0}^{+}}{lim }f(x) = L$

II. Giới hạn hữu hạn của hàm số tại vô cực

ĐỊNH NGHĨA 3

a. Cho hàm số $y=f(x)$ xác định trên khoảng $(a; +\infty )$

Ta nói hàm số $y=f(x)$ có giới hạn là số L khi $x\rightarrow +\infty$ nếu với dãy số $(x_{n})$bất kì, $x_{n}>a; x_{n}\rightarrow +\infty$

ta có $f(x_{n})\rightarrow L$

Kí hiệu: $\underset{x\rightarrow +\infty }{lim }f(x) = L$ hay $f(x)\rightarrow L$khi $x\rightarrow +\infty $

b. Cho hàm số $y=f(x)$ xác định trên khoảng $(-\infty ;a)$

Ta nói hàm số $y=f(x)$ có giới hạn là số L khi $x\rightarrow -\infty$ nếu với dãy số $(x_{n})$bất kì, \(x_{n}

ta có $f(x_{n})\rightarrow L$

Kí hiệu: $\underset{x\rightarrow -\infty }{lim }f(x) = L$ hay $f(x)\rightarrow L$khi $x\rightarrow -\infty $

CHÚ Ý

a. Với c, k là các hằng số và k là nguyên dương, ta luôn có:

$\underset{x\rightarrow +\infty }{lim }c = c$
$\underset{x\rightarrow -\infty }{lim }c = c$
$\underset{x\rightarrow +\infty }{lim }\frac{c}{x^{k}} = 0$
$\underset{x\rightarrow -\infty }{lim }\frac{c}{x^{k}} = 0$

b. Định lí 1 về giới hạn của hàm số khi $x\rightarrow x_{0}$ vẫn còn đúng khi $x\rightarrow +\infty $hoặc $x\rightarrow -\infty$

III. Giới hạn vô cực của hàm số

1. Giới hạn vô cực

ĐỊNH NGHĨA 4

Cho hàm số $y=f(x)$ xác định trên khoảng $(a; +\infty )$

Ta nói hàm số $y=f(x)$ có giới hạn là $-\infty $khi $x\rightarrow +\infty $nếu với dãy số $(x_{n})$bất kì, $x_{n}>a$và $x_{n}\rightarrow +\infty $ta có $f(x_{n})\rightarrow -\infty$

Kí hiệu: $\underset{x\rightarrow +\infty }{lim }f(x) = -\infty$ hay $f(x)\rightarrow -\infty $khi $x\rightarrow +\infty $

NHẬN XÉT: $\underset{x\rightarrow +\infty }{lim }f(x) = +\infty \Leftrightarrow \underset{x\rightarrow +\infty }{lim }(-f(x)) = -\infty$

2. Một vài giới hạn đặc biệt

$\underset{x\rightarrow +\infty }{lim }x^{k} = +\infty$ với k nguyên dương.
$\underset{x\rightarrow -\infty }{lim }x^{k} = -\infty$ nếu k là số lẻ
$\underset{x\rightarrow -\infty }{lim }x^{k} = +\infty$ nếu k là số chẵn

3. Một vài quy tắc về giới hạn vô cực

Nếu $\underset{x\rightarrow x_{0}}{lim }f(x) = L\neq 0$ và $\underset{x\rightarrow x_{0}}{lim }g(x) = +\infty $(hoặc $-\infty $)thì $\underset{x\rightarrow x_{0}}{lim }f(x)g(x)$được tính theo quy tắc cho trong bảng sau:

a. Quy tắc tìm giới hạn của tích $f(x).g(x)$

$\underset{x\rightarrow x_{0}}{lim }f(x)$	$\underset{x\rightarrow x_{0}}{lim }g(x)$	$\underset{x\rightarrow x_{0}}{lim }f(x)g(x)$
$L>0$	$+\infty$	$+\infty$
$L>0$	$-\infty$	$-\infty$
$L<0$	$+\infty$	$-\infty$
$L<0$	$-\infty$	$+\infty$

b. Quy tắc tìm giới hạn của thương $\frac{f(x)}{g(x)}$

$\underset{x\rightarrow x_{0}}{lim }f(x)$	$\underset{x\rightarrow x_{0}}{lim }g(x)$	Dấu của $g(x)$	$\underset{x\rightarrow x_{0}}{lim }\frac{f(x)}{g(x)}$
$L$	$\pm \infty$	Tùy ý	0
$L>0$	0	+	$+\infty$
$L>0$		-	$-\infty$
$L<0$		+	$-\infty$
$L<0$		-	$+\infty$

(Dấu của $g(x)$ xét trên một khoảng K nào đó đang tính giới hạn, với $x\neq x_{0}$

CHÚ Ý: Các quy tắc trên vẫn đúng cho các trường hợp $x\rightarrow x_{0}^{+}, x\rightarrow x_{0}^{-}, x\rightarrow +\infty ; x\rightarrow -\infty$

B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI

Câu 1: trang 132 sgk toán Đại số và giải tích 11

Dùng định nghĩa tìm các giới hạn sau:

a) $\underset{x\rightarrow 4}{lim}\frac{x+1}{3x - 2}$ ;

b) $\underset{x \rightarrow +\infty }{lim}\frac{2-5x^{2}}{x^{2}+3}$ .

=> Xem hướng dẫn giải

Câu 2: trang 132 sgk toán Đại số và giải tích 11

Cho hàm số

$f(x) = \left\{ \matrix{
\sqrt x + 1 \text{ nếu }x\ge 0 \hfill \cr
2x\text{ nếu }x < 0 \hfill \cr} \right.$

Và các dãy số $(u_n)$ với $u_n= \frac{1}{n}$, $(v_n)$ với $v_n= -\frac{1}{n}$.

Tính $\lim u_n$ , $\lim v_n$, $\lim f (u_n)$ và $\lim (v_n)$.

Từ đó có kết luận gì về giới hạn của hàm số đã cho khi $x → 0$ ?

=> Xem hướng dẫn giải

Câu 3: trang 132 sgk toán Đại số và giải tích 11

Tính các giới hạn sau:

a) $\underset{x\rightarrow -3}{lim}$ $\frac{x^{2 }-1}{x+1}$;	b) $\underset{x\rightarrow -2}{lim}$ $\frac{4-x^{2}}{x + 2}$;
c) $\underset{x\rightarrow 6}{lim}$ $\frac{\sqrt{x + 3}-3}{x-6}$;	d) $\underset{x\rightarrow +\infty }{lim}$ $\frac{2x-6}{4-x}$;
e) $\underset{x\rightarrow +\infty }{lim}$ $\frac{17}{x^{2}+1}$;	f) $\underset{x\rightarrow +\infty }{lim}$ $\frac{-2x^{2}+x -1}{3 +x}$.

=> Xem hướng dẫn giải

Câu 4: trang 132 sgk toán Đại số và giải tích 11

Tính các giới hạn sau:

a) $\underset{x\rightarrow 2}{lim}$ $\frac{3x -5}{(x-2)^{2}}$;

b) $\underset{x\rightarrow 1^{-}}{lim}$ $\frac{2x -7}{x-1}$;

c) $\underset{x\rightarrow 1^{+}}{lim}$ $\frac{2x -7}{x-1}$.

=> Xem hướng dẫn giải

Câu 5: trang 133 sgk toán Đại số và giải tích 11

Cho hàm số $f(x) = \frac{x+2}{x^{2}-9}$ có đồ thị như trên hình 53.

a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi $x → -∞$ , $x → 3^-$ và $x → -3^+$

b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

$\underset{x\rightarrow -\infty }{\lim} f(x)$ với $f(x)$ được xét trên khoảng $(-\infty; -3)$,

$\underset{x\rightarrow 3^{-}}{\lim} f(x)$ với $f(x)$ được xét trên khoảng $(-3,3)$,

$\underset{x\rightarrow -3^{+}}{lim} f(x)$ với $f(x)$ được xét trên khoảng $(-3; 3)$.

=> Xem hướng dẫn giải

Câu 6: trang 133 sgk toán Đại số và giải tích 11

Tính:

$\eqalign{
& a)\mathop {\lim }\limits_{x \to + \infty } ({x^4} - {x^2} + x - 1) \cr
& b)\mathop {\lim }\limits_{x \to - \infty } ( - 2{x^3} + 3{x^2} - 5) \cr
& c)\mathop {\lim }\limits_{x \to - \infty } (\sqrt {{x^2} - 2x + 5}) \cr
& d)\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} + 1} + x} \over {5 - 2x}} \cr} $

=> Xem hướng dẫn giải

Câu 7: trang 133 sgk toán Đại số và giải tích 11

Một thấu kính hội tụ có tiêu cự là $f$ . Gọi $d$ và $d'$ lần lượt là khoảng cách từ một vật thật $AB$ và từ ảnh $A'B'$ của nó tới quang tâm $O$ của thấu kính (h.54). Công thức thấu kính là $\frac{1}{d}+\frac{1}{d'}=\frac{1}{f}.$

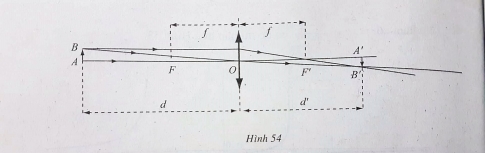
a) Tìm biểu thức xác định hàm số $d' = φ(d)$ .

b) Tìm $\underset{d\rightarrow f^{+} }{\lim} φ(d)$ , $\underset{d\rightarrow f^{-} }{\lim} φ(d)$ và $\underset{d\rightarrow +\infty }{\lim} φ(d)$. Giải thích ý nghĩa của các kết quả tìm được.

=> Xem hướng dẫn giải

=> Trắc nghiệm đại số và giải tích 11 bài 2: Giới hạn của hàm số (P2)

23 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Đại số và giải tích lớp 11

a) $\underset{x\rightarrow -3}{lim}$ \(\frac{x^{2 }-1}{x+1}\);	b) $\underset{x\rightarrow -2}{lim}$ \(\frac{4-x^{2}}{x + 2}\);
c) $\underset{x\rightarrow 6}{lim}$ \(\frac{\sqrt{x + 3}-3}{x-6}\);	d) $\underset{x\rightarrow +\infty }{lim}$ \(\frac{2x-6}{4-x}\);
e) $\underset{x\rightarrow +\infty }{lim}$ \(\frac{17}{x^{2}+1}\);	f) $\underset{x\rightarrow +\infty }{lim}$ \(\frac{-2x^{2}+x -1}{3 +x}\).

Giải bài 2: Giới hạn của hàm số

A. Tóm tắt lý thuyết

B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI

Kiến thức thú vị

Xem thêm bài viết khác