Trắc nghiệm đại số 10 chương 2: Hàm số bậc nhất và bậc hai (P1)

Bài có đáp án. Bộ bài tập trắc nghiệm toán 10 đại số chương 2: Hàm số bậc nhất và bậc hai (P1). Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.

Câu 1: Cho hàm số f(x) = − |x| .Khẳng định nào sau đây là đúng.

• A. f(x) là hàm số lẻ
• B. f(x) là hàm số chẵn
• C. Đồ thị của hàm số f(x) đối xứng qua gốc tọa độ
• D. Đồ thị của hàm số f(x) đối xứng qua trục hoành

Câu 2: Cho hàm số y = f(x) = a + bx + c. Rút gọn biểu thức f(x + 3)– 3f(x + 2) + 3f(x + 1) ta được:

• A. a – bx – c
• B. a + bx – c
• C. a – bx + c
• D. a + bx + c

Câu 3: Cho hai điểm A, B thõa mãn hệ phương trình Tìm m để đường thẳng AB cắt đường thẳng y = x + m tại điểm C có tọa độ thỏa mãn $y_{C} = x^{2}_{C}$.

• A. m = 2
• B. m = 1
• C. m = 0
• D. m = 2 ±

Câu 4: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng P(n) = 360 − 10n (gam). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để khối lượng cá sau một vụ thu được nhiều nhất?

• A. 12
• B. 18
• C. 36
• D. 40

Câu 5: Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0; 2), B(−2; 5), C(3; 8)

• A. y = + $\frac{1}{10}$x − 2
• B. y = − $\frac{1}{10}$x + 2
• C. y = − $\frac{1}{10}$x − 2
• D. y = + $\frac{1}{10}$x + 2

Câu 6: Hàm số y = xác định trên [0; 1) khi:

• A. m <
• B. m 1
• C. m < hoặc m $\geq$ 1
• D. m 2 hoặc m < 1

Câu 7: Xác định các hệ số a và b để Parabol (P) : y = có đỉnh I(−1; −5).

• A.
• B.
• C.
• D.

Câu 8: Tìm m để hàm số y = − 2x + 2m + 3 có giá trị nhỏ nhất trên đoạn [2 ; 5] bằng -3.

• A. m = −3q
• B. m = −9
• C. m = 1
• D. m = 0

Câu 9: Tìm điểm M(a; b) với a < 0 nằm trên Δ : x + y − 1 = 0 và cách N(−1; 3) một khoảng bằng 5. Giá trị của a − b là:

• A. 3
• B. −1
• C. −11
• D. 1

Câu 10: Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết d đi qua A(1; 3), B(2; −1)

• A. y = −4x + 2
• B. y = −2x + 3
• C. y = −4x + 5
• D. y = −4x + 7

Câu 11: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f(x) = − 4x + 3 trên đoạn [−2; 1] .

• A. M = 15; m = 1
• B. M = 15; m = 0
• C. M = 1; m = −2
• D. M = 0; m = −15

Câu 12: Tìm các giá trị thực của tham số m để hàm số y = xác định trên (−1; 2).

• A.
• B. m ≤ −1 hoặc m ≥ 2
• C. m < −1 hoặc m > 2
• D. −1 < m < 2

Câu 13: Xét tính đồng biến, nghịch biến của hàm số f(x) = − 4x + 5 trên khoảng (−∞; 2) và trên khoảng (2; +∞). Khẳng định nào sau đây đúng?

• A. Hàm số nghịch biến trên (−∞; 2), đồng biến trên (2; +∞).
• B. Hàm số đồng biến trên (−∞; 2), nghịch biến trên (2; +∞).
• C. Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞).
• D. Hàm số đồng biến trên các khoảng (−∞; 2) và (2; +∞).

Câu 14: Tìm m ∈ Z để hai đường thẳng y = mx + 1 (d1) và y = 2x + 3 (d2) cắt nhau tại một điểm có tọa độ nguyên.

• A. m = 2
• B. m ∈ {0; 1; 3; 4}
• C. m ∈ {0; 2}
• D. m ∈ {±1; ±2}

Câu 15: Cho hàm số y = f(x) có bảng biến thiên như sau:

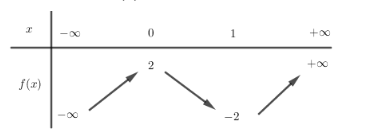
Với giá trị nào của tham số m thì phương trình |f(x) − 1| = m có bốn nghiệm phân biệt.

• A. m = 1
• B. 1 < m < 3
• C. 0 < m < 1
• D. m ≥ 3

Câu 16: Đồ thị sau đây biểu diễn hàm số nào?

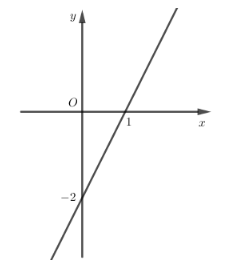
• A. y = 2x − 2
• B. y = x − 2
• C. y = −2x − 2
• D. y = −x − 2

Câu 17: Cho parabol (P) : y = − 4x + 3 và đường thẳng d : y = mx + 3. Tìm tất cả các giá trị thực của m để d cắt (P) tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng $\frac{9}{2}$.

• A. m = 7
• B. m = −7
• C. m = −1, m = −7
• D. m = −1

Câu 18: Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 (triệu đồng) và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phảiđịnh giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.

• A. 30 triệu đồng
• B. 29 triệu đồng
• C. 30,5 triệu đồng
• D. 29,5 triệu đồng

Câu 19: Cho điểm A (1; 1) và hai đường thẳng (d1) : y = x − 1; (d2) : y = 4x − 2 . Viết phương trình đường thẳng (d) đi qua điểm A và cắt các đường thẳng (d1), (d2) tạo thành một tam giác vuông.

• A. y = 2x – 1
• B. y = –2x + 3
• C. y = -x + 2 hoặc
• D. Không xác định được

Câu 20: Cho đường thẳng d : y = (m − 1) x + m và d′: y = (m2 − 1) x + 6. Tìm m để hai đường thẳng d, d′ song song với nhau

• A. m = 0 và m = 3
• B. m = 0 và m = 2
• C. m = 0 và m = 1
• D. m = 0 và m = 4