Trắc nghiệm đại số 9 bài 2: Đồ thị của hàm số y = ax^2 (a ≠ 0)

Bài có đáp án. Câu hỏi và bài tập trắc nghiệm bài 2: Đồ thị của hàm số y = ax^2 (a ≠ 0) Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.

Câu 1: Parabol(P) là đồ thị của hàm số nào sau đây

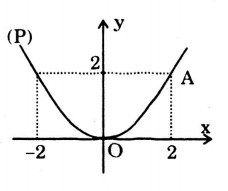
• A.
• B.
• C.
• D.

Câu 2: Parabol (P) là đồ thị của hàm số nào sau đây?

• A.
• B.
• C.
• D.

Câu 3: Trong mặt phẳng tọa độ Oxy, lấy bốn điểm M(1;), N($\sqrt{3};\sqrt{6}$), E($-\sqrt{3};3\sqrt{2}$), F($-\sqrt{2};4\sqrt{2}$) thì điểm nào thuộc đồ thị của hàm số $y=\sqrt{2}{x}^2$

• A. Điểm M và N
• B. Điểm E và F
• C. Điểm M và E
• D. Điểm N và F

Câu 4: Gọi (P) là đồ thị của hàm số ($m\ne 3$). Tính m cho biết (P) đi qua điểm I($\sqrt{3};\sqrt{6}$)

• A.
• B.
• C.
• D. Một kết quả khác

Câu 5: Cho điểm M có hoành độ x= -2 thuộc đồ thị (P) của hàm số . Tọa độ điểm M' là điểm đối xứng của M qua trục tung là:

• A. M'(2;-2)
• B. M'(2;2)
• C. M'(4;-2)
• D. M'(-2;4)

Câu 6: Tọa độ giao điểm của parabol (P): và đường thẳng (D): y=2x là:

• A.(1;4) và (0;0)
• B.(-2;4) và (0;0)
• C.(0;0) và (-1;2)
• D.(0;0) và (2;4)

Câu 7: Tọa độ giao điểm cả parabol và đường thẳng (D) y=-3 là:

• A. và $(\sqrt{3};-3)$
• B. và $(-\sqrt{6};-3)$
• C. và $(-\sqrt{6};3)$
• D. và $(\sqrt{3};-\sqrt{2})$

Câu 8: Xét bài toán :" cho hàm số có đồ thị (P). Nêu cách vẽ điểm M trên (P) có hoành độ là $x_M=\sqrt{2}$"

Hãy sắp xếp một cách hợp lí các câu sau để có lời giải của bài toán trên

A. Vẽ cung tròn (O;OA) cắt trục Ox tại B

B. Vẽ đồ thị (P) trong mặt phẳng tọa độ Oxy

C. Vẽ điểm A có tọa độ (1;1)

C. Qua B vẽ đường thẳng vuông góc với Ox cắt (P) tại điểm M. Đó là điểm ta cần vẽ.

Sắp xếp nào sau đây hợp lí nhất:

• A. A,B,D,C
• B. B,A,C,D
• C. B,C,A,D
• D. D,C,B,A