Giải bài 1: Hàm số lượng giác
Đây là bài học mở đầu cho chương hàm số lượng giác và phương trình lượng giác. Bài học giới thiệu cho ta tập xác định, tính tuần hoàn, sự biến thiên và đồ thị của các hàm số lượng giác.
A. Lý thuyết
I. Hàm số 
TXĐ:
Nhận xét: Hàm số là hàm số lẻ và tuần hoàn với chu kì $2 \pi$ và $-1 \leq \sin x \leq 1$ hay nói cách khác là tập giá trị của hàm số này là $[-1;1]$.
Đồ thị hàm số trên $\mathbb{R}$
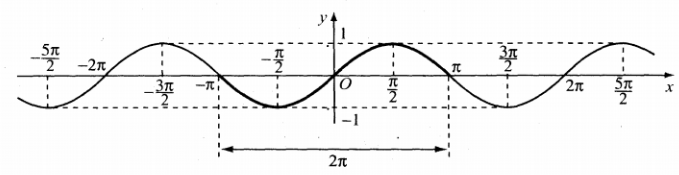
ll. Hàm số .
TXĐ: .
Nhận xét: Hàm số là hàm số chẵn và tuần hoàn với chu kì $2 \pi$ và $-1 \leq \cos x \leq 1$ hay nói cách khác là tập giá trị của hàm số này là $[-1;1]$.
Đồ thị hàm số trên $\mathbb{R}$ (tịnh tiến đồ thị hàm số theo vecto $\overrightarrow{u}=(-\frac{\pi}{2};0))$
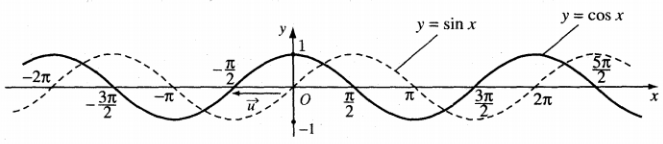
lll. Hàm số
TXĐ: .
Nhận xét: Hàm số là hàm số lẻ và tuần hoàn với chu kì $\pi$. Tập giá trị của hàm là $\mathbb{R}$.
Đồ thị hàm số
lV. Hàm số .
TXĐ: .
Nhận xét: Hàm số là hàm số lẻ và tuần hoàn với chu kì $\pi$. Tập giá trị của hàm số là khoảng $(-\infty, +\infty)$.
Đồ thị hàm số
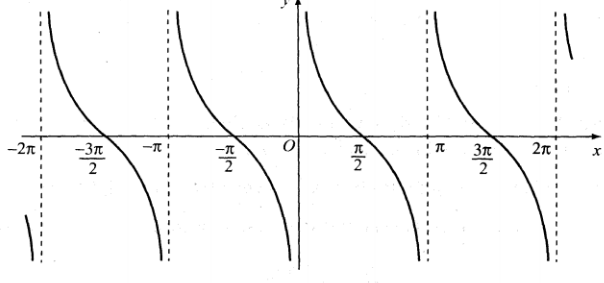
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
Bài 1: Trang 17 sgk - đại số và giải tích 11
Hãy xác định các giá trị của x trên đoạn để hàm số $y=\tan x$
a) Nhận giá trị bằng 0.
b) Nhận giá trị bằng 1.
c) Nhận giá trị dương.
d) Nhận giá trị âm.
Bài 2: Trang 17 sgk - đại số và giải tích 11
Tìm tập xác định của hàm số
a) .
b) .
c) .
d) .
Bài 3: Trang 17 sgk - đại số và giải tích 11
Dựa vào đồ thị hàm số y = sinx, hãy vẽ đồ thị của hàm số y = |sinx|
Bài 4: Trang 17 sgk - đại số và giải tích 11
Chứng minh rằng sin2(x + kπ) = sin 2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y = sin2x.
Bài 5: Trang 17 sgk - đại số và giải tích 11
Dựa vào đồ thị hàm số y = cosx, tìm các giá trị của x để .
Bài 6: Trang 17 sgk - đại số và giải tích 11
Dựa vào đồ thị hàm số y = sinx, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương.
Bài 7: Trang 18 sgk - đại số và giải tích 11
Dựa vào đồ thị hàm số , tìm khoảng giá trị của x để hàm số đó nhận giá trị âm.
Bài 8: Trang 18 sgk - đại số và giải tích 11
Tìm giá trị lớn nhất của hàm số:
a) ;
b) .
=> Trắc nghiệm đại số và giải tích 11 bài 1: Hàm số lượng giác (P2)
Lớp 11