Giải bài 3: Các hệ thức lượng trong tam giác và giải tam giác
Bài học giới thiệu nội dung: Các hệ thức lượng trong tam giác và giải tam giác . Một kiến thức không quá khó song đòi hỏi các bạn học sinh cần nắm được phương pháp để giải quyết các bài toán. Dựa vào cấu trúc SGK toán lớp 10, KhoaHoc sẽ tóm tắt lại hệ thống lý thuyết và hướng dẫn giải các bài tập 1 cách chi tiết, dễ hiểu. Hi vọng rằng, đây sẽ là tài liệu hữu ích giúp các em học tập tốt hơn
A. Tổng hợp kiến thức
1. Định lí Côsin
- Trong tam giác ABC bất kì với
, ta có:
|
Hệ quả
|
2. Định lí sin
- Trong tam giác ABC bất kì với , R là bán kính đường tròn ngoại tiếp ,ta có:
|
3. Công thức tính diện tích tam giác
- Cho tam giác ABC bất kì với , R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác ; $p=\frac{a+b+c}{2}$ là nửa chu vi tam giác , ta có :
|
Đặc biệt:
- Dựa vào hệ thức lượng trong tam giác , ta có thể áp dụng để giải tam giác cũng như việc đo đạc ở thực tế.
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
Câu 1: Trang 59 - sgk hình học 10
Cho tam giác ABC vuông tại A, và cạnh a = 72cm. Tính $\widehat{C}$, cạnh b và đường cao h.
Câu 2: Trang 59 - sgk hình học 10
Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc .
Câu 3: Trang 59 - sgk hình học 10
Cho tam giác ABC có , cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc $\widehat{B} , \widehat{C}$ của tam giác đó.
Câu 4: Trang 59 - sgk hình học 10
Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.
Câu 5: Trang 59 - sgk hình học 10
Cho tam giác ABC có . Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.
Câu 6: Trang 59 - sgk hình học 10
Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.
a) Tam giác đó có góc tù không?
b) Tính độ dài trung tuyến MA của tam giác ABC đó.
Câu 7: Trang 59 - sgk hình học 10
Tính góc lớn nhất của tam giác ABC biết:
a) Các cạnh a = 3cm, b = 4cm và c = 6cm;
b) Các cạnh a = 40cm, b = 13cm, c = 37cm.
Câu 8: Trang 59 - sgk hình học 10
Cho tam giác ABC biết cạnh a = 137,5cm, và $\widehat{C}=57^{\circ}$. Tính góc A, bán kính R của đường tròn ngoại tiếp, cạnh b và c của tam giác.
Câu 9: Trang 59 - sgk hình học 10
Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n.
Chứng minh rằng: .
Câu 10: Trang 60 - sgk hình học 10
Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ra nhìn chiều cao AB của tháp dưới các
góc và $\widehat{BQA}=48^{\circ}$. Tính chiều cao của tháp.
Câu 11: Trang 60 - sgk hình học 10
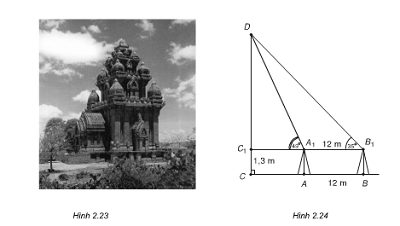
Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm cùng thẳng hàng với $C_{1}$ thuộc chiều cao CD của tháp. Người ta đo được $\widehat{DA_{1}C_{1}}=49^{\circ}$ và$\widehat{DB_{1}C_{1}}=35^{\circ}$. Tính chiều cao CD của tháp đó.
=> Trắc nghiệm hình học 10 bài 3: Các hệ thức lượng trong tam giác và giải tam giác( P2)
Lớp 10