Cách nhận xét biểu đồ hộp Ôn tập Địa 10
Cách nhận xét biểu đồ hộp được Khoahoc sưu tầm và đăng tải. Biểu đồ hộp là một loại biểu đồ thể hiện các khuôn hình của dữ liệu định tính, để tìm hiểu thêm định nghĩa cũng như đặc trưng của biểu đồ hộp, cách đọc biểu đồ hộp các em cùng tham khảo nội dung chính của bài học hôm nay, mời các em cùng tham khảo.
Cách nhận xét biểu đồ hộp lớp 10
Biểu đồ hộp (Box Plot)
Định nghĩa
Biểu đồ hộp trong tiếng Anh là Box Plot hay Box and Whisker plot, là một loại biểu đồ thể hiện các khuôn hình của dữ liệu định tính (quantitative data).
Biểu đồ hộp do John Tukey sáng tạo ra năm 1977.
Biểu đồ hộp (Box plot) hay còn gọi là biểu đồ hộp và râu (Box and whisker plot) là biểu đồ diễn tả 5 vị trí phân bố của dữ liệu, đó là: giá trị nhỏ nhất (min), tứ phân vị thứ nhất (Q1), trung vị (median), tứ phân vị thứ 3 (Q3) và giá trị lớn nhất (max).
Đặc trưng của biểu đồ hộp
- Biểu đồ hộp giúp biểu diễn các đại lượng quan trọng của dãy số như giá trị nhỏ nhất (min), giá trị lớn nhất (max), tứ phân vị (quartile), khoảng biến thiên tứ phân vị (Interquartile Range) một cách trực quan, dễ hiểu.
- Trên biểu đồ hộp, ngoài các đại lượng số trung bình, trung vị, còn thể hiện một số thông số sau:
(1) Số phân tử hay còn gọi là tứ phân vị (Quartiles): Tứ phân vị là đại lượng mô tả sự phân bố và sự phân tán của tập dữ liệu. Số phân tử có 3 giá trị, đó là số phân tử thứ nhất (Q1), thứ nhì (Q2) và thứ ba (Q3). Ba giá trị này chia một tập hợp dữ liệu (đã sắp xếp dữ liệu theo trật từ bé đến lớn) thành 4 phần có số lượng quan sát đều nhau.
Tứ phân vị được xác định như sau:
+ Sắp xếp các số theo thứ tự tăng dần
+ Cắt dãy số thành 4 phần bằng nhau
+ Tứ phân vị là các giá trị tại vị trí cắt

(2) Khoảng biến thiên số phân tử (Interquartile Range - IQR) IQR được xác định như sau:

Cách đọc hiểu biểu đồ boxplots
Trung vị được biểu thị bằng đường thẳng đứng ở giữa cái hộp. Trong ví dụ trên, trung vị nằm giữa 4 và 6, xấp xỉ 5
Thêm vào đó, biểu đồ boxplot còn thể hiện 2 đại lượng phổ biến khi nói về độ rộng của một tập dữ liệu:
- Khoảng dữ liệu (range): Nếu bạn quan tâm đến độ rộng của tất cả dữ liệu thì, đó đơn giản là khoảng cách giữa giá trị lớn nhất và giá trị nhỏ nhất trong tập dữ liệu. Còn nếu bạn muốn loại trừ các giá trị ngoại lai, thì đó là khoảng cách giữa 2 đầu ria mép!
- Khoảng liên phần tư (IQR): là nửa giữa của tập dữ liệu nằm giữa 2 điểm Q3 và Q1. Trong biểu đồ trên, IQR là khoảng 7 – 3 = 4
Và cuối cùng, biểu đồ boxplots còn cung cấp thông tin cho chúng ta về hình dạng của tập dữ liệu:
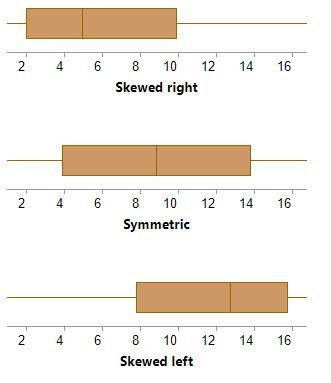
Đây là 3 hình dạng chủ yếu về độ lệch. Nếu đường trung vị chia chiếc hộp thành 2 nửa đều nhau, thì tập dữ liệu này đối xứng (symmetric). Nếu nửa phải lớn hơn (nửa trái) thì tập dữ liệu bị lệch phải (right-skewed), và ngược lại, nếu nửa trái lớn hơn thì tập dữ liệu bị lệch trái (left-skewed).
Ví dụ
Xét một ví dụ về việc sử dụng biểu đồ hộp:
Dưới đây mô tả sử dụng biểu đồ hộp để phân tích, nhận biết vấn đề.
Ví dụ, với số liệu thu thập được về tỉ lệ làm lại (Rework Ratio) trong quá trình sản xuất, (có xmin = 0,0; Q1 = 14,9; x = 19,0; x = 15,8; Q3 = 20,6; xmax =23,2) ta có biểu đồ hộp với hình dáng biểu đồ như sau:
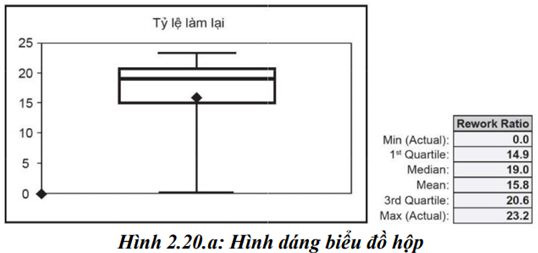
Trung bình tỉ lệ làm lại là 15,8%, trung vị là 19%.
Dữ liệu có xu hướng nghiêng nhiều về phía trên giá trị trung bình.
Khoảng số phân tử = Q3 - Q1 = 20,6 - 14,9 = 5,7
Khoảng cách giữa giá trị lớn nhất và nhỏ nhất là 23,2 - 0 = 23,2.
Nhìn chung, tỉ lệ làm lại cao và quá trình có sự dao động lớn, không ổn định, kiểm soát chất lượng kém. Tuy nhiên, biểu đồ hộp giúp nhìn trực quan hơn khi so sánh 3 giai đoạn hoặc khu vực khác nhau như hình dưới đây:
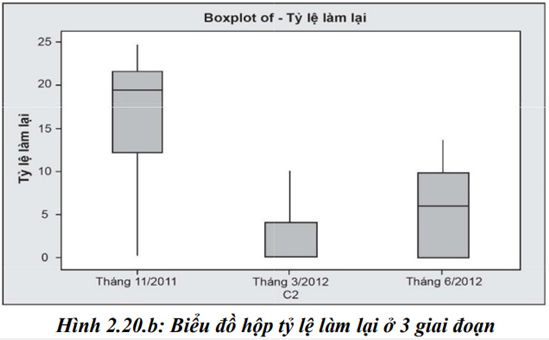
Nhận xét:
Với ba lần thu thập dữ liệu về tỉ lệ làm lại vào thời điểm tháng 11/2011, tháng 3/2012 và tháng 6/2012, dữ liệu vào thời điểm tháng 11/2011 cho thấy quá trình kiểm soát lỗi kém vì xu hướng tập trung của dữ liệu (trung vị) ở mức cao, độ dao động lớn.
Kiểm soát chất lượng vào thời điểm tháng 3/2012 là tốt nhất vì dữ liệu về tỉ lệ làm lại tập trung ở mức thấp, dao động ở phạm vi hẹp.
Cách nhận xét biểu đồ hộp được Khoahoc chia sẻ trên đây. Hy vọng sẽ giúp ích cho các em nắm được nội dung của bài đồng thời chuẩn bị tốt cho bài giảng sắp tới. Chúc các em học tốt, ngoài ra các em có thể tham khảo thêm các môn học khác đều có tại, tài liệu học tập lớp 10
Xem thêm bài viết khác
- Trình bày ưu điểm và nhược điểm của giao thông vận tải đường sắt Ôn tập Địa 10
- Đặc điểm nào sau đây không đúng với ngành nội thương Ôn tập Địa 10
- Đặc điểm nào sau đây không đúng với ngành công nghiệp? Ôn tập Địa 10
- Phân biệt gia tăng dân số tự nhiên và gia tăng dân số cơ học? Ôn tập Địa 10
- Vai trò của rừng Amazon Ôn tập Địa 10
- Giao thông vận tải là ngành có vai trò rất quan trọng gì Ôn tập Địa 10
- Soạn bài Viết một bản hướng dẫn nơi công cộng Chân trời sáng tạo Soạn Văn 10 tập 1 - Chân trời sáng tạo
- Soạn bài Viết một bản nội quy nơi công cộng Chân trời sáng tạo Soạn Văn 10 tập 1 - Chân trời sáng tạo
- Soạn bài Huyện Trìa, Đề Hầu, Thầy Nghêu mắc lỡm Thị Hến Chân trời sáng tạo Soạn Văn 10 tập 1 - Chân trời sáng tạo
- Soạn bài Xã trưởng-mẹ Đốp Chân trời sáng tạo Soạn Văn 10 tập 1 - Chân trời sáng tạo
- Soạn bài Thực hành tiếng Việt trang 127 Chân trời sáng tạo Soạn Văn 10 tập 1 - Chân trời sáng tạo












 Ôn tập Địa 10
Ôn tập Địa 10